Ustalenie prawidłowej ceny produktu czy usługi jest jednym z największych, a jednocześnie najważniejszych wyzwań detalisty na konkurencyjnym rynku. Zbyt niska cena zmniejsza przychody a w konsekwencji zysk. Z kolei cena zbyt wysoka ogranicza popyt i również powoduje zmniejszenie przychodów. Wprawdzie jednostkowy zysk na sprzedaży jest wyższy, ale może nie skompensować strat związanych ze zmniejszeniem wolumenu.
Ustalenie optymalnej ceny produktu – od czego zacząć?
Trudności związane z ustaleniem optymalnej ceny towarów wynikają z liczby i złożoności czynników, które mają na nią wpływ. Są to między innymi ceny produktów komplementarnych i substytucyjnych. Do listy można dopisać także promocje, reklamy, aktywność i ofertę konkurencji, sytuację ekonomiczną klientów, ich gusta i preferencje, koszty zakupu towarów, kwestie związane z logistyką. Dodatkowe wyzwania wiążą się z produktami, na których popyt ma charakter sezonowy i wynika np. z uwarunkowań pogodowych. Klasycznym przykładem takiego asortymentu są lody, na które popyt związany jest ściśle z temperaturą powietrza. Inne tego typu produkty, które można wymienić to okulary przeciwsłoneczne, narty, napoje chłodzące, kurtki zimowe, stroje kąpielowe, usługi hotelowe, przeloty turystyczne.
Paradoks ceny
W przypadku tego rodzaju produktów często mamy do czynienia z paradoksem ceny. Klasyczna ekonomiczna teoria popytu i podaży mówi, że im wyższa cena, tym mniejszy popyt na towar lub usługę. Zazwyczaj tak jest. Jednak w przypadku produktów wybitnie sezonowych zależność ta może ulec zachwianiu. Często się przecież zdarza, że najwyższe ceny notowane są w szczycie sezonu na dany produkt. A więc wtedy, gdy i sprzedaż jest najwyższa. Sprzedawcy wiedząc, że konsumenci właśnie w tym okresie najbardziej potrzebują produktu i są najbardziej skłonni do zakupów, wykorzystują to, podnosząc ceny. Sytuację tego rodzaju ilustruje wykres poniżej. Widać delikatną, ale wyraźną pozytywną relację między ceną (oś pozioma) a sprzedawanym wolumenem (oś pionowa).
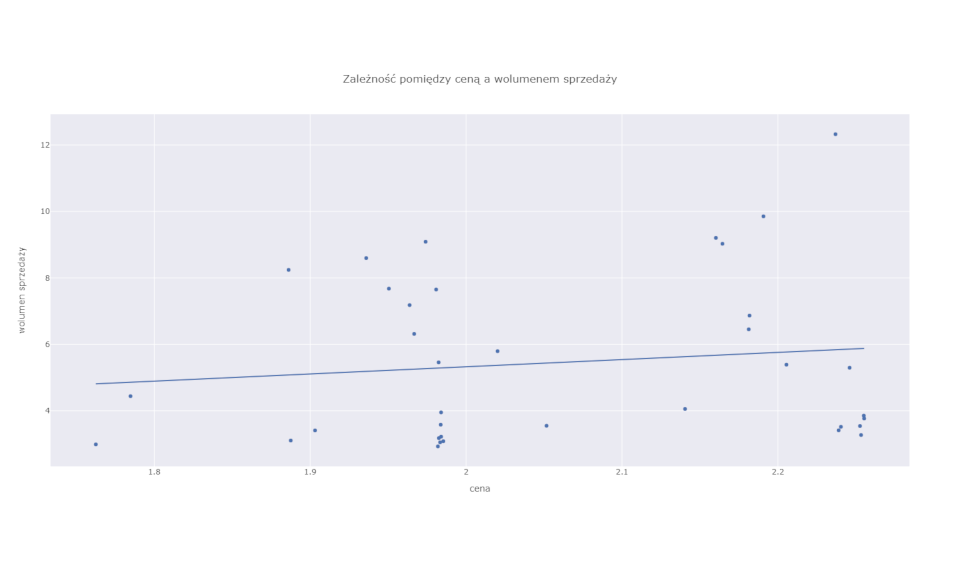
Patrząc tylko na ten wykres, będący w istocie prostym modelem cena-popyt, można byłoby wyciągnąć naiwny wniosek, że podnoszenie cen powoduje wzrost sprzedaży. Jak wiadomo nie jest to prawda (za wyjątkiem bardzo wąskiej i specyficznej grupy dóbr luksusowych). Podnosząc ceny lodów w okresie od października do marca, nie uda nam się zwiększyć ich sprzedaży.
Zależność obserwowana na wykresie jest efektem splotu dwóch czynników. Po pierwsze jest to wpływ ceny i temperatury powietrza na sprzedaż, a po drugie wpływ temperatury (sezonu) na cenę. Ten ostatni wiąże się właśnie z decyzjami sprzedawcy o dostosowaniu ceny do podwyższonego popytu.
Czy istnieje idealne narzędzie do estymacji ceny?
Rozwiązanie zagadki rzeczywistego wpływu ceny na sprzedaż wymaga więc nieco bardziej złożonego podejścia niż analiza korelacji między ceną a popytem (której przykład ilustrował poprzedni wykres). Idealnym narzędziem do estymacji tego rodzaju efektów są losowe eksperymenty (np. testy A/B). W teorii można sobie wyobrazić, że detalista będzie losowo zmieniał ceny tak, aby przetestować różne warianty i połączenia – co zaowocuje np. podwyższeniem ceny lodów w grudniu, czy jej drastyczną obniżką w wyjątkowo upalnym czerwcu. W praktyce jednak jest to trudno wykonalne, a jeżeli już to na niewielką skalę i w ograniczonym czasie. Jest to bowiem bardzo kosztowny eksperyment.
Sprzedaż produktów po nieoptymalnej cenie powoduje drenaż przychodów. Dodatkowo częste i nieprzewidywalne zmiany cen mogą negatywnie wpływać na doświadczenie konsumentów i skłaniać ich do przechodzenia do konkurencji. Praktycznym rozwiązaniem jest więc wykorzystanie danych, które już mamy i które nie pochodzą z eksperymentu do estymacji wpływu interesującego nas czynnika (w tym wypadku ceny) na istotny dla nas rezultat (w tym wypadku sprzedaż). Jest to możliwe, choć trzeba zaznaczyć, że nie jest to zadanie trywialne i wymaga rozbudowanego aparatu matematycznego. W dzisiejszym artykule nie będę się jednak skupiał na matematycznych, statystycznych i filozoficznych niuansach związanych z analizą przyczynowości. Zamiast tego pokażę możliwe do uzyskania wyniki tego rodzaju analizy i ich praktyczne efekty.
Sezonowość a cena produktu
Rozwiązanie wymaga na początku nałożenia na dane „modelu” odzwierciedlającego nasze rozumienie sposobu funkcjonowania systemu, który chcemy analizować. Potrzebny jest przy tym zarówno zdrowy rozsądek, jak i wiedza ekspercka. Nasze założenia możemy opisać przy pomocy grafu, jak na ilustracji poniżej.

Przede wszystkim, jak widać, ustalamy założenia, co do kierunku oddziaływania poszczególnych zmiennych. Cena zmienia się pod wpływem temperatury (a dokładniej przez działania detalisty wynikającego z jego wiedzy odnośnie wpływu temperatury na zachowania konsumentów). Detalista zmieniając cenę, nie jest zaś w stanie zmienić temperatury powietrza – myślę, że nie jest to kontrowersyjne założenie – stąd strzałka skierowana jest tylko w jedną stronę. Temperatura ma także bezpośredni wpływ na sprzedaż (kiedy jest ciepło więcej ludzi ma ochotę na lody). Dodatkowo uwzględniamy, że wpływ na cenę i na sprzedaż mogą mieć także inne czynniki, które pozostają poza naszą obserwacją. Jest to oczywiście bardzo uproszczony model i z łatwością można go rozbudować o kolejne czynniki wpływające na cenę lub sprzedaż.
Estymacja faktycznego wpływu ceny na sprzedaż
Na podstawie tak sformułowanego modelu oraz danych historycznych o cenie, wolumenie i temperaturze, przy pomocy zaawansowanych metod analitycznych, możliwa jest estymacja faktycznego wpływu ceny na sprzedaż. Innymi słowy możemy oszacować, w jakim stopniu zmiana ceny jest przyczyną zmiany wolumenu sprzedaży. Stąd już tylko krok do wykorzystania tej wiedzy w praktyce i optymalizacji ceny.
Poniższy przykład pokazuje proces poszukiwania optymalnej ceny lodów w miesiącu wrześniu przy prognozowanej średniej temperaturze dobowej 14,2 st. C. Możemy podobne wykresy wygenerować dla dowolnej wartości temperatury, co ma akurat w tym przypadku duże znaczenie. Inna będzie bowiem optymalna cena, gdy wrzesień będzie wyjątkowo ciepły, a inna gdy będą padały rekordy chłodu.

Wrzesień jest miesiącem przejściowym pomiędzy szczytem sezonu a okresem jesienno-zimowym. Do tej pory detalista tradycyjnie utrzymywał jeszcze we wrześniu dość wysokie ceny produktu. Na osi poziomej wykresu pokazujemy zmianę ceny w stosunku do ceny bazowej – oznacza ją linia 0 w okolicy środka wykresu. Niebieska krzywa pokazuje jak zmieniają się przychody ze sprzedaży w zależności od przyjętej ceny. Przesuwając się na prawo od linii 0 (czyli podwyższając cenę) obserwujemy spadek przychodów. Wyższa cena negatywnie wpływa na popyt, a większy przychód jednostkowy nie kompensuje spadku wolemu. Przesuwając się w lewo od linii 0, obserwujemy wzrost przychodów, chociaż tylko do pewnego punktu. Za nim, zwiększony wolumen sprzedaży, przestaje kompensować spadek ceny. Ten punkt oznacza punkt optymalnej ceny – oznaczony pionową linią przerywaną. Model sugeruje, że optymalna cena jest o 80 groszy niższa od dotychczasowej ceny bazowej.
Zastosowanie się do rekomendacji i obniżenie ceny powoduje wzrost obrotów o nieco ponad 26% w stosunku do scenariusza bazowego. Obrazuje to poniższy wykres.

Przedstawiona w artykule metoda daje olbrzymie możliwości, wykorzystując najnowsze osiągniecia badawcze w dziedzinie sztucznej inteligencji i analizie przyczynowej. W praktyce oczywiście dla większej dokładności model powinien uwzględnić także dodatkowe czynniki takie jak ceny innych produktów, ceny u konkurencji, reklamy, ulotki, gazetki, oferty, promocje, czynniki makroekonomiczne. Pełne rozwiązanie daje także o wiele bardziej dogłębny wgląd w sytuację. Symulacja wpływu decyzji cenowych na wolumen i przychody ze sprzedaży pomaga podejmować lepsze decyzje. Te z kolei przekładają się na wymierne efekty finansowe i mogą dać istotną przewagę konkurencyjną.